The trigonotable

At some point during the high school, one is required to memorize the value of some trigonometric functions. In this post, I'm going to show an easy trick to memorize the following table:

and also some intuition if our memory fails for some value. To do so, we need to remember what the sine and cosine mean. While the tagent has its own meaning, today let's just simplify to the formula:

\[\tan(x) = \frac{\sin(x)}{\cos(x)}\]

Build by pieces – memorization method

Everyone has its own methods for memorizing. Here I'm going to explain one that has been really useful to me. I've never read any book explaining this, but I suspect that probably it is a standard and well-known method.

When I was going to the high school, I had to memorize the features of textual genres. At that degree of maturity, I remember that all that information was completely meaningless to me, but I needed to somehow put it all in my mind. What I finally did (and luckily it worked) was to build words and sentences, or stories from the initials of the features I needed to remember. This way, since I knew where I had to end up, it was a way to deduce or better remember the different pieces, i.e. the feature of e.g the argumentative genre.

In the problem at hand we have something similar. We have a table, and we are going to deduce a way to build it, so that at the end we get it built with little effort. First, we will write a symbolic "divided by two" in every cell, like this:

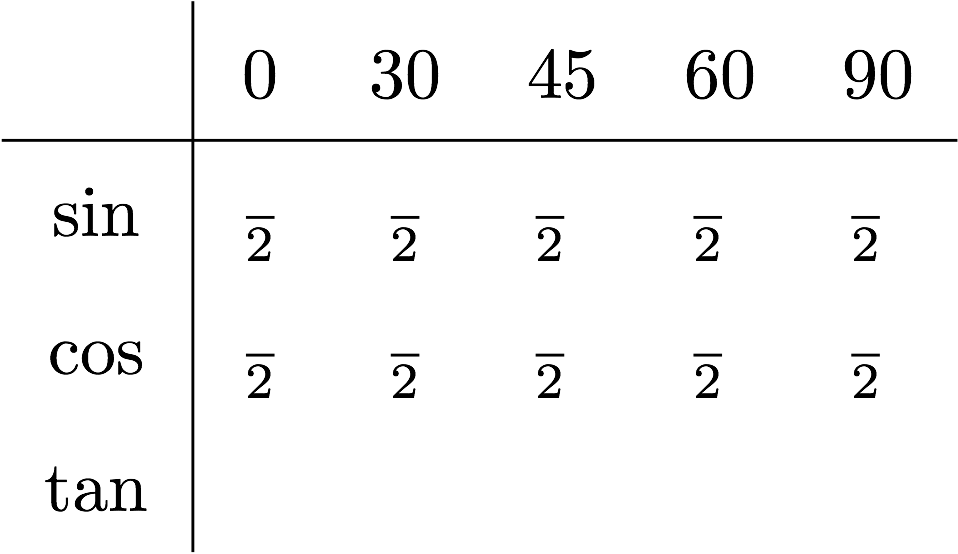
Easy isn't it? Ok, now write from left to right the square root of the numbers from 0 to 4 in every cell of the sine, and the other way around for the cosine:

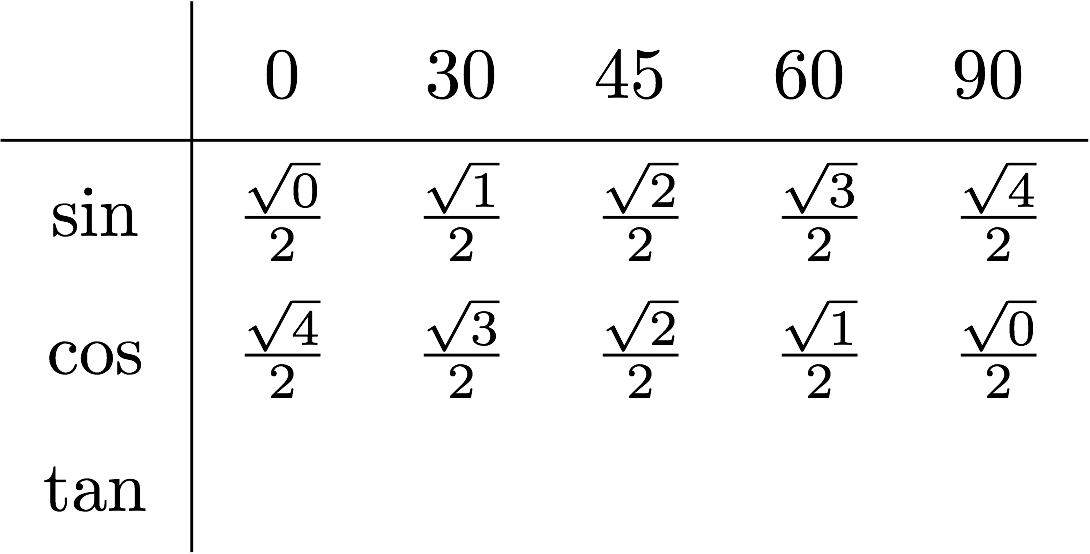
Simplifying the numbers, you'll discover that you end up with the first table at the beginning of the post, and the tangent can be obtained just dividing the first row by the second row.

Height and width of circles – intuition method

The last method is useful to keep the knowledge in mind, but we actually understand nothing about what the sine and cosine are. To this end, consider the following image:

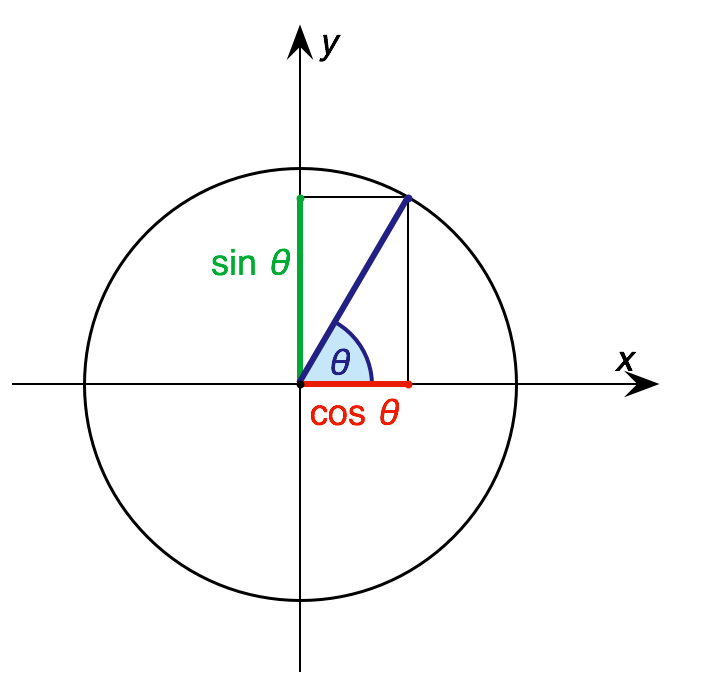
In plain words, for each possible angle, the cosine means the length of the triangle base, whereas the sine represents its length. This interpretation allows us to understand many things:

• In the first quadrant, when the angle is small the cosine is large, and the sine is small. The other way around when the angle approaches 90. This explains why the sine grows with the angle, and the cosine decreases.
• The angle of 45º is the only one where the sine and cosine have the same value and it’s a kind of inflection value. While it’s difficult to memorize the values of the tangent, the value of 45º it’s easy because it’s just equal to 1.
• While they are not in the table, angles larger than 90º lead to sine or cosine (or both) negative. Specifically, in the second quadrant the cosine is negative, in the third both, and in the fourth the sine is negative.

Conclusion

Today we have reviewed a well-known table of the values of sine and cosine for typical angle values. While it may look complicated to memorize, I have shown a method to build the table, and also an intuition that can help us during this process or to validate our memory. While the level of this post is for high school students, I think that a review for mature students is always good just to keep fresh these easy concepts. If you liked this post please click on like, thanks!