Interference Alignment

In the last blog post, I explained the concept of Zero Forcing, either at the transmitter (also known as null steering) or the receiver. Mathematically, it is based on computing the null space of some matrix, whose existence (for completely random entries as in this case) depends on the dimensions of that matrix. In turn, the matrix dimensions depend on the number of antennas at the transmitter and the receiver. Therefore, Zero Forcing will only be feasible for antenna settings where the corresponding null space exists. Otherwise, other approaches may be used:

• Use less antennas at the transmitter or the receiver. Obviously, this is usually non-optimal.
• Time-sharing: use a round-robin scheme to alleviate the number of users to be removed per round

For the Broadcast and Multiple Access channels introduced in the last post, the tools we have reviewed so far are enough to obtain the optimal degrees of freedom. However, there exist other scenarios where this is not always true, and it is when Interference Alignment (IA) gives us the opportunity to attain (or at least approach to) the channel DoF.

Interference Channel

Let's then review this scenario, since it is the first one where IA was shown to provide a boost in the DoF.

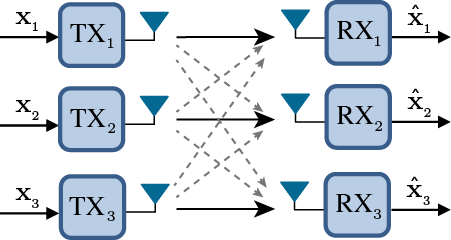
Now there are $K$ transmitter-receiver pairs, who only communicate with each other, so they receive interference containing messages intended to other users. They can be equipped with multiple antennas and then apply linear transformations via precoding and receiving filters as shown for null-steering and zero-forcing techniques.

Results

Surprisingly, the IA approach shows that considering an arbitrary number of pairs of users $K$ with the same number of antennas $M$ at transmitters and receivers, the DoF sum is $KM/2$. This means that independently of the number of users, we can achieve the same performance per user!

Ok, nice…but how?

I'm going to explain the simplest scenario where IA can be applied, in which there are 3 users, each node is equipped with 2 antennas, and every user will be able to transmit one message.

If you are interested, it's interesting to see that with ZF concepts we cannot achieve more than 2 DoF, by turning off one of the pairs, and one receiving antenna per user. However, neglecting resources is not usually a good idea.

Let's assume that each transmitter $i$ uses a 2x1 precoding vector $\mathbf{v}_i$ to transmit the symbol ${x_i}$. Then, the signal obtained at receiver $j$ can be written as:

\begin{equation} \displaystyle \mathbf{y}_i = \mathbf{H}_{j1} \mathbf{v}_1 x_1 + \mathbf{H}_{j2} \mathbf{v}_2 x_2 + \mathbf{H}_{j3} \mathbf{v}_3 x_3 + \mathbf{n}_i    \end{equation}

where $\mathbf{H}_{ji}$ is the 2x2 matrix whose entries are channel gains from each antenna of transmitter $i$ to receiver $j$, and $\mathbf{n}_i$ is the noise term.

Let's consider that the values for the precoding vectors are randomly chosen. Then we would have the following situation:

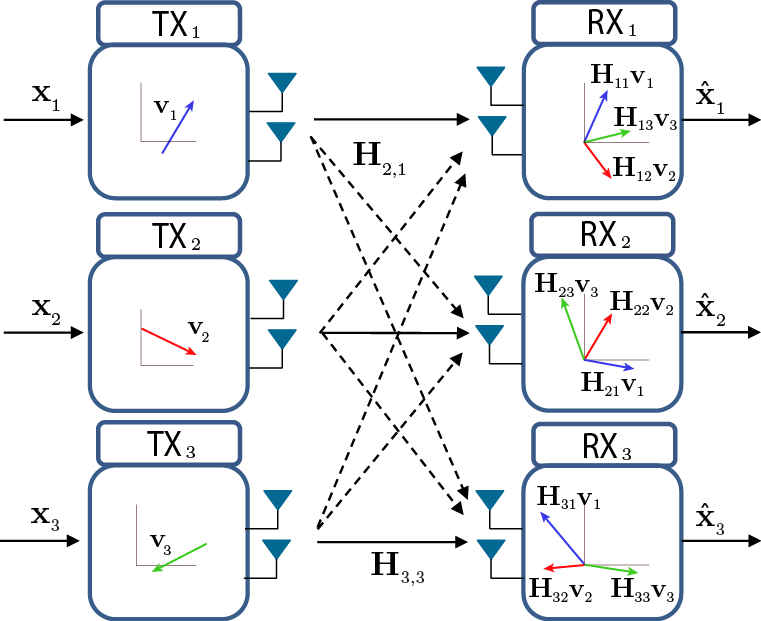
This is problematic, since we have to resolve 3 messages, but we only have 2 equations (one for each receiving antenna).

The interesting idea here is that we are not actually interesting in resolving all the messages at all the receivers, only one. Then, it's not a problem for us if the two interference symbols are observed mixed. So, a let's assume that there is a way to transmit the symbols such that they are received as follows:

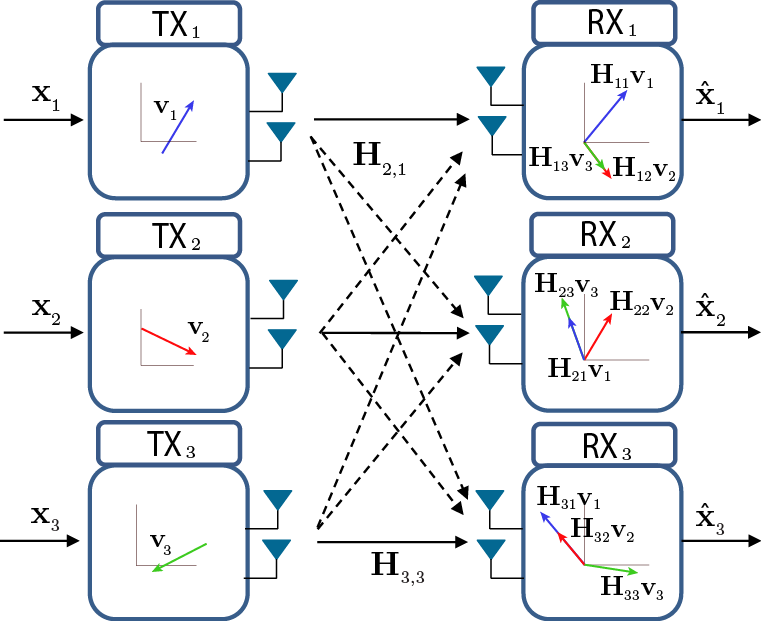
In this situation, we can resolve at each receiver the desired symbol, and also a combination of the interference, which is not interesting and we can just drop it. Intrinsically, we have been able to resolve the desired messages, thanks to the fact that the interference is \textit{aligned}. In other words, the two vectors representing the interference at each receiver, are collapsed to a subspace of one dimension, or a line. Since we have two dimensions to allocate 3 signals, compressing the two interference signals to one dimension leaves one dimension free to allocate the desired signal.

The mathematical formulation for IA in this case is as simple as

\begin{equation} \begin{matrix} \mathbf{H}_{12} \mathbf{V}_2 = \mathbf{H}_{13} \mathbf{V}_3 \
\mathbf{H}_{21} \mathbf{V}_1 = \mathbf{H}_{23} \mathbf{V}_3 \
\mathbf{H}_{31} \mathbf{V}_1 = \mathbf{H}_{32} \mathbf{V}_2    \end{matrix} \end{equation}

but in general would be

\begin{equation} \mathsf{span} \left( \mathbf{H}_{12} \mathbf{V}_2 \right) = \mathsf{span} \left( \mathbf{H}_{13} \mathbf{V}_3 \right) \
\mathsf{span} \left( \mathbf{H}_{21} \mathbf{V}_1\right) = \mathsf{span} \left( \mathbf{H}_{23} \mathbf{V}_3\right) \
\mathsf{span} \left( \mathbf{H}_{31} \mathbf{V}_1\right) = \mathsf{span} \left( \mathbf{H}_{32} \mathbf{V}_2 \right)   \end{equation}

where $\mathsf{span}$ refers to the subspace generated, so we actually only need that the subspace generated is the same, but it's easier  to equate the operands to find a closed-form solution. Since the objective of these posts is to see the main ideas and concepts behind my research in academia, I'm not going to enter into mathematical details, and I refer you to my thesis and the original paper by Cadambe and Jafar.

Conclusion

In this post I have introduced the idea of Interference Alignment, as a way of looking at the wireless transmissions from a different perspective. The main idea is that we need to reduce the number of variables to resolve the equations we have, and consequently obtain the desired variables. In our case the equations are observations at each receiving antenna, and the variables are the messages transmitted to the different users. To reduce variables, we transmit the signals in such a way the interference is mixed (aligned) at the receivers, thus releasing enough spatial dimensions for desired signals to be resolved without interference.

While this has been a very introductory description of Interference Alignment, I think that it's enough to catch the concept, and could motivate you to continue this journey in the study of wireless communications. After 10 years, there are still many research papers using IA, and many questions still to be answered in the research community where IA could have a principal role.

IA as explained here was the main topic in my master's thesis. However, it is assumed that we know the channels perfect and instantaneously, which is something not really realistic, specially in scenarios where the terminals are moving, e.g. travelling in a train. In the next posts I will explain how this concept can be applied to the case where we have delayed information of the channel, which is the door to understand a bit more about my Phd thesis. Likes and comments welcome!