DC: Dungeon & Code

Today I come with a fairly easy but interesting problem. Consider a dungeon grid like this:

Ok, we will have something much more simplified, e.g:

XXXXXXXXX..e..XXXXXXXX
XXXXX……………………XXXXX
XXX………….XXX…….s…..XXX
XXXXX……………………XXXXX
XXXXXXXXXXXXXXXXXXX

This array of strings can represent somehow the previous dungeon, where each character is a position, “s” is the starting position, “e” the ending one, and “X” the obstacles, so positions that cannot be landed.

The objective will be to find an algorithm to get the shortest path from start to end positions. Instantly, when we see shortest path we think on Dijkstra algorithm, basically because is the first result when googling it. The problem is that we don't have a graph. Hence, once transformed to a graph this problem is fairly easy. I refer you to my code in Github for this conversion and the rest of this post will be devoted to the Dijkstra algorithm through an example. As always any doubts about the code, more than happy to help.

Dijsktra Algorithm: an example

I'm not going to create a new long tutorial on this algorithm, because there are thousands over the Internet. Just give a visual example of how this works.

Consider we have a graph like the one next:

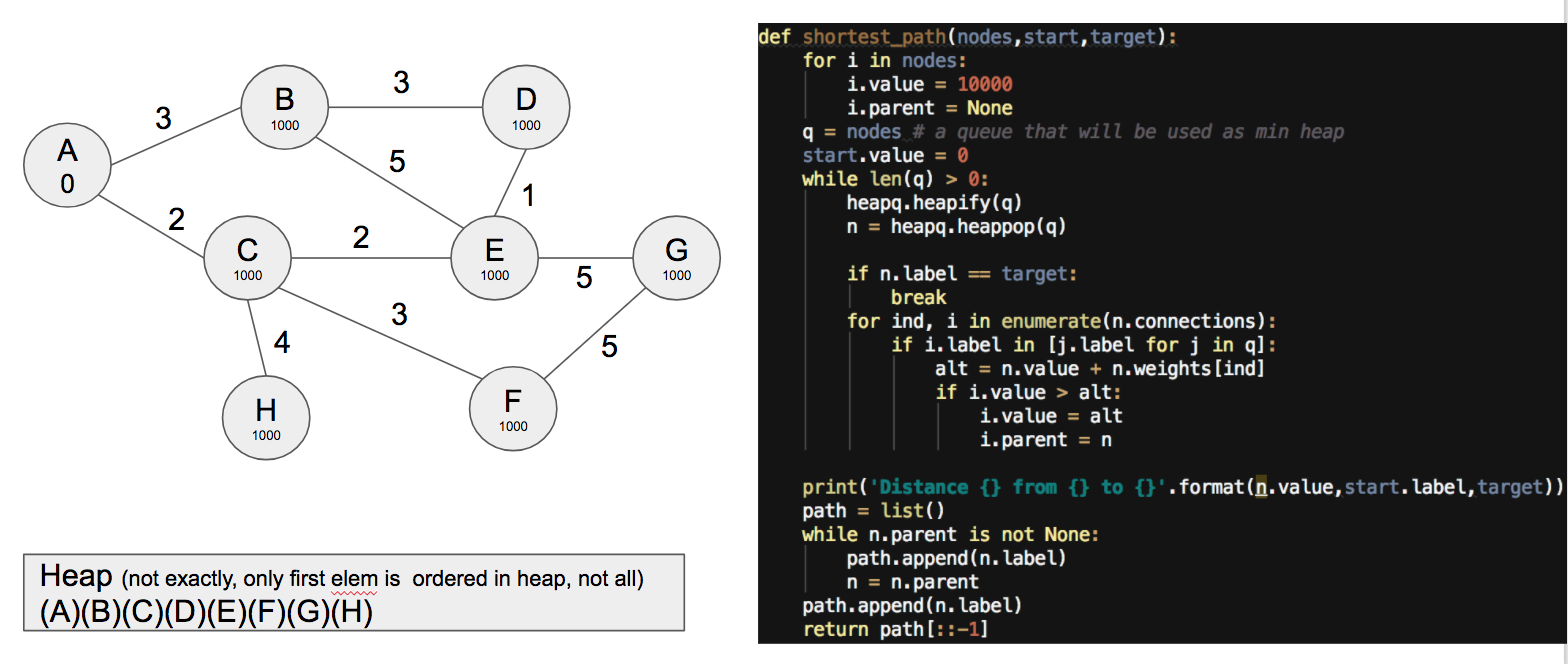
where every node initially is at a big distance from A except A itself. Number in edges represent the distance between each pair of nodes. Note than in our example distance is one for each pair of positions, so this example addresses a more general case.

To solve the shortest path from A to G, we need a heap. A heap is data structure very useful in computer science where items are appended in such a way that you can get the maximum or minimum of the list in constant time (i.e. independent of the list length). This strictly doesn't mean that the list is ordered (as noted in the image), though I will show it ordered to simplify.

On the right hand side I have the code with the algorithm. So let's try to follow it. In the first iteration we select A and for each of its neighbors compute the distance to A, obtaining:

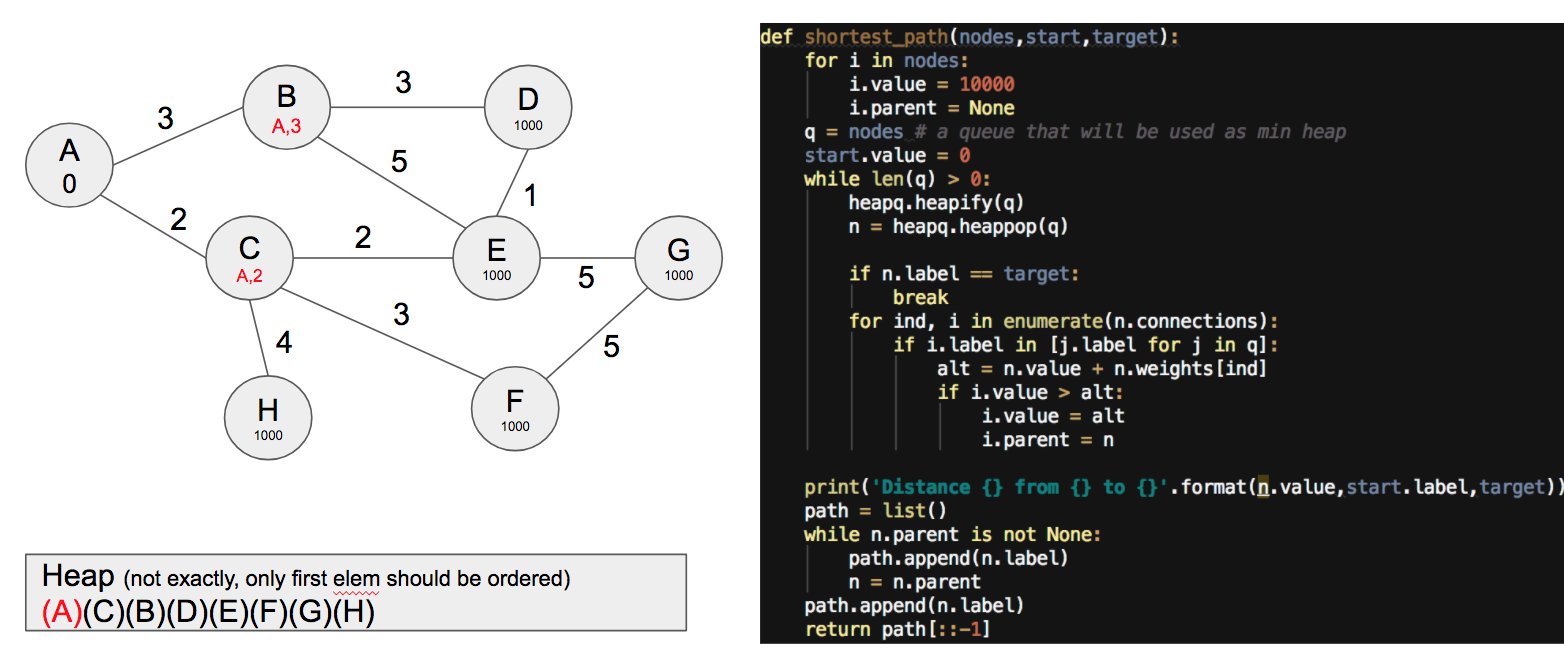
Notice that I've saved the best way to arrive from A to B and from A to C, together with the distance (in the code this is saved in the attribute parent).

Then, the following minimum becomes C, so for each neighbor we compute the distance from A to this node by summing 2 (the distance from A to C) plus the distance from C to this node. This is done for all neighbors except A, which is no more in the heap. This is a way to save computation time, omitting the nodes already visited. The graph after processing C looks as follows:

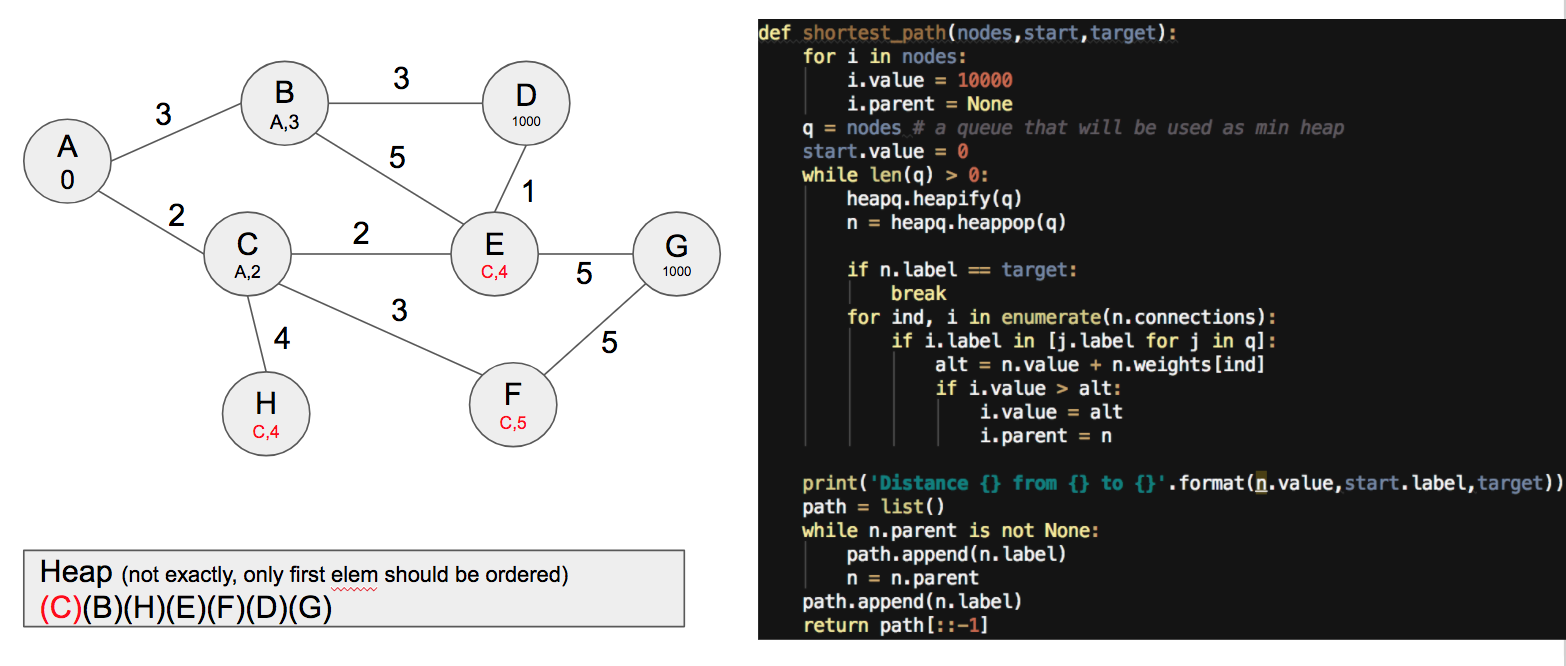
Now a human probably would go with E, because it's closer to G and has a reasonable short distance of 4. However, following the algorithm the following node to extract is B. This ensures that all possibles paths are explored so that the solution is optimal.

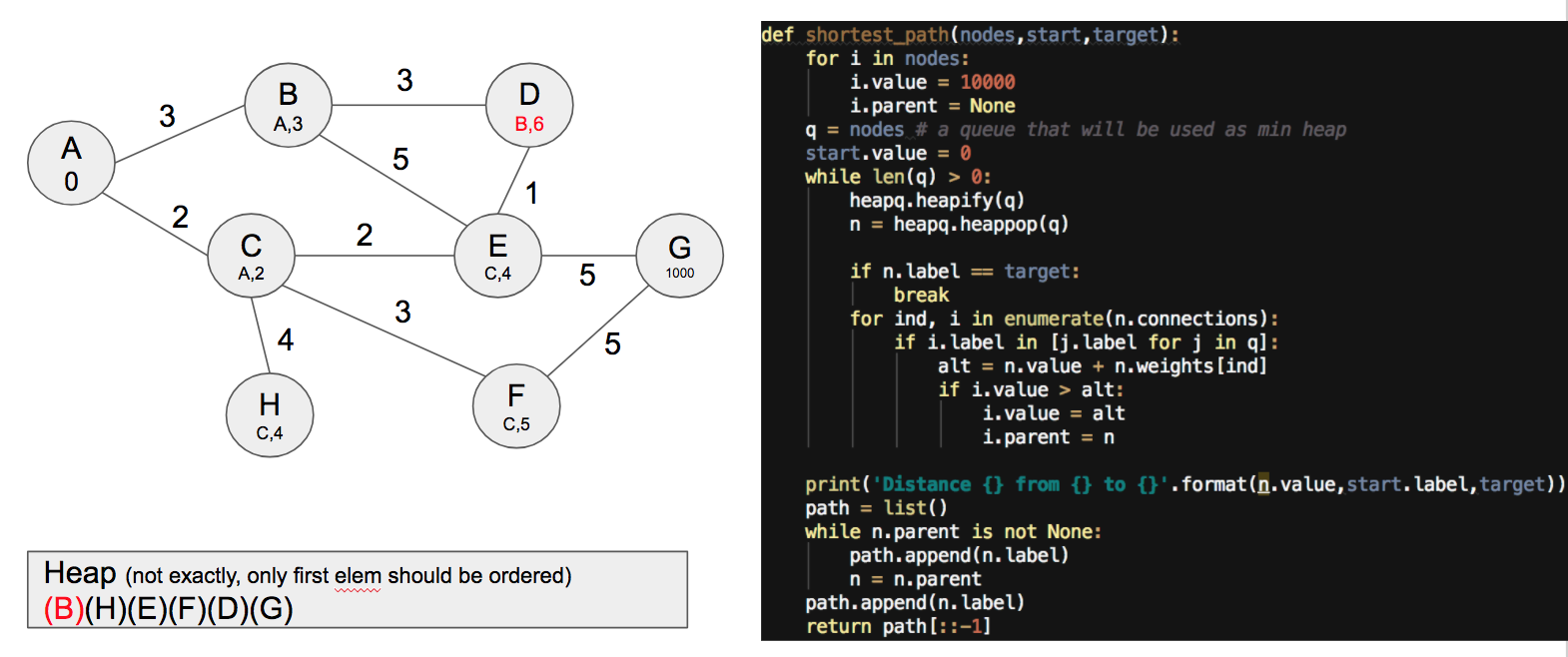
This is an interesting iteration, since we can see that node E has not been modified as it's faster moving there from C than from B. Next move could be either of H or E, but in this case we select H and nothing changes.

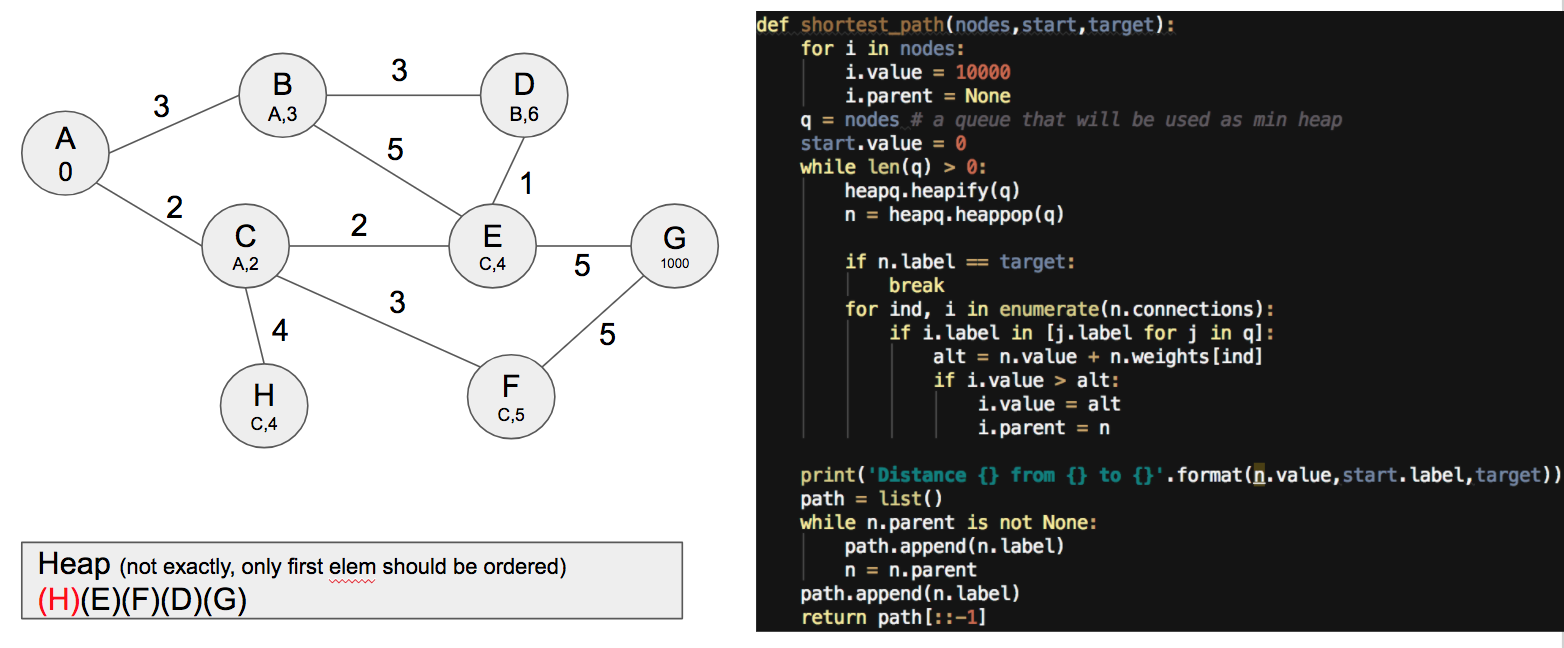
After that, we select E:

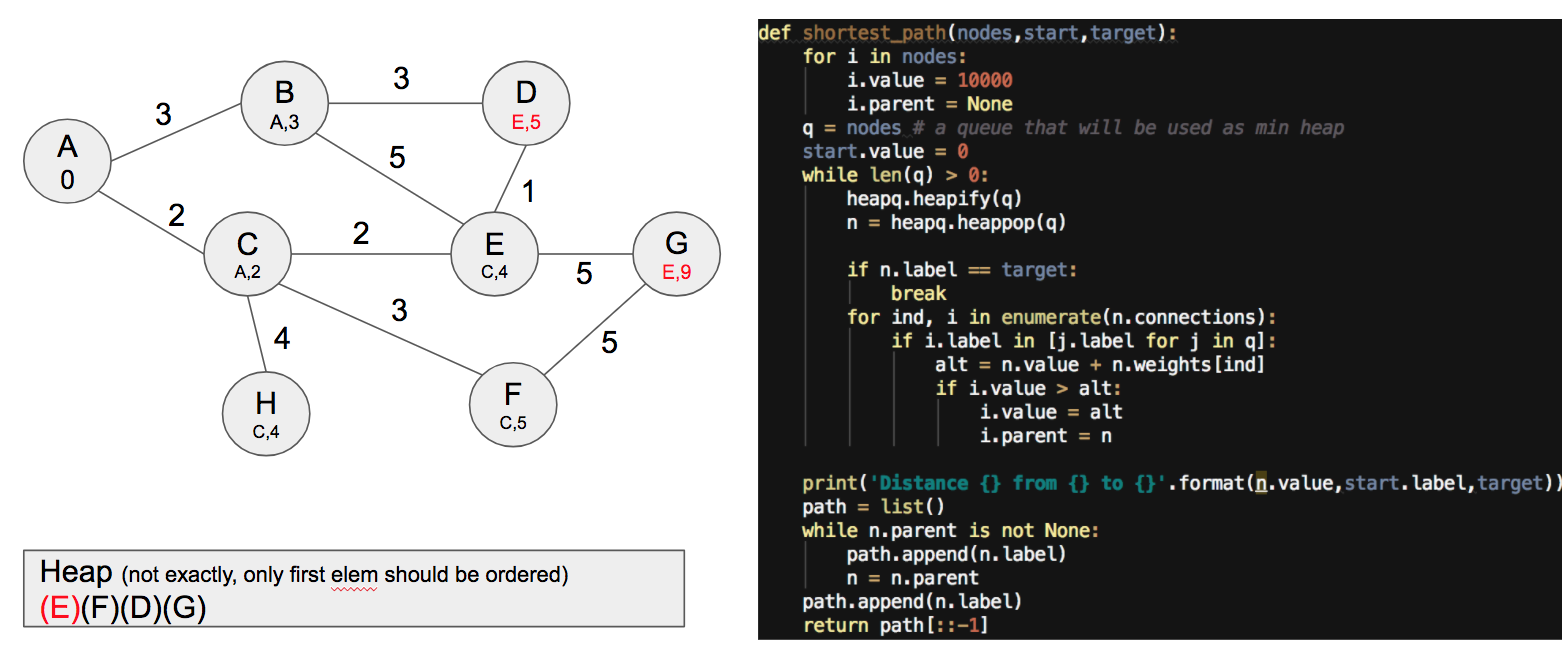
But notice that we need to end up with the elements in the heap, even though nothing changes, to ensure there are no better solutions. I just show you the state of the graph for all those iterations.

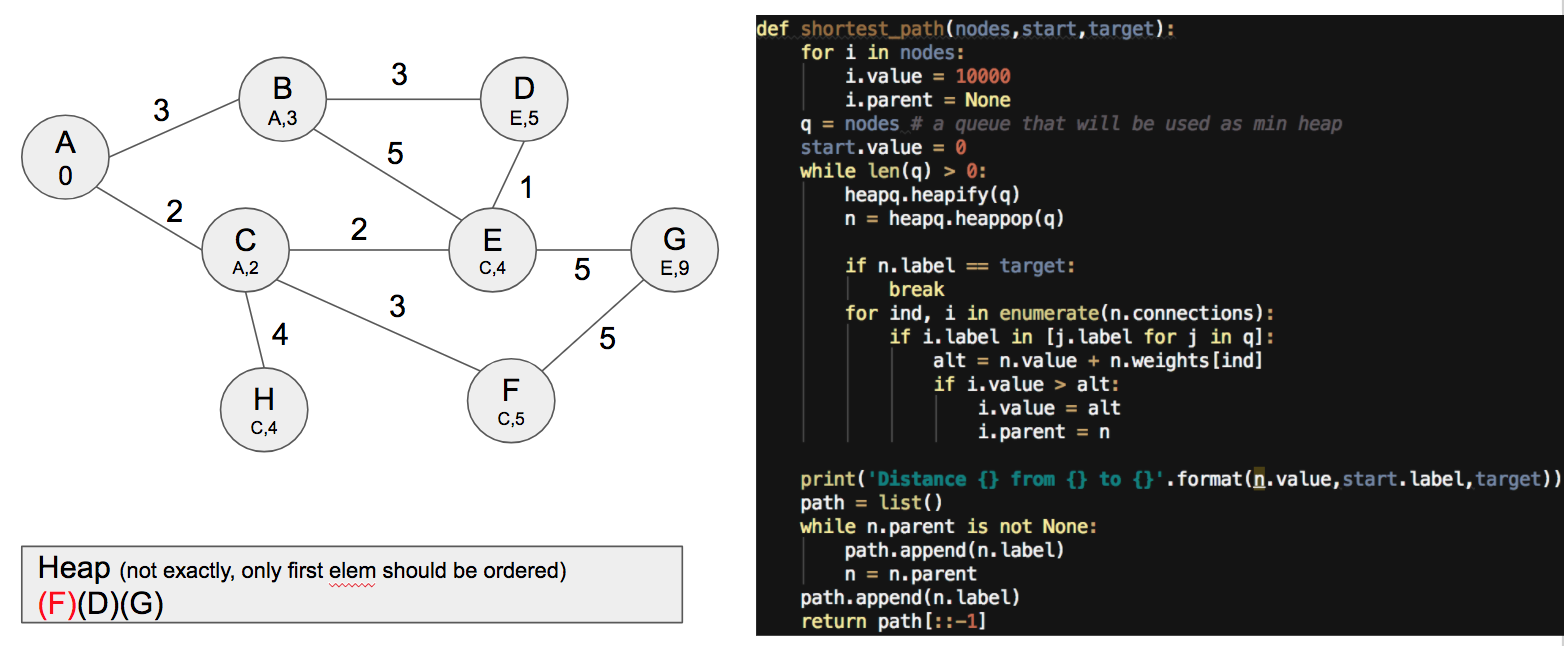
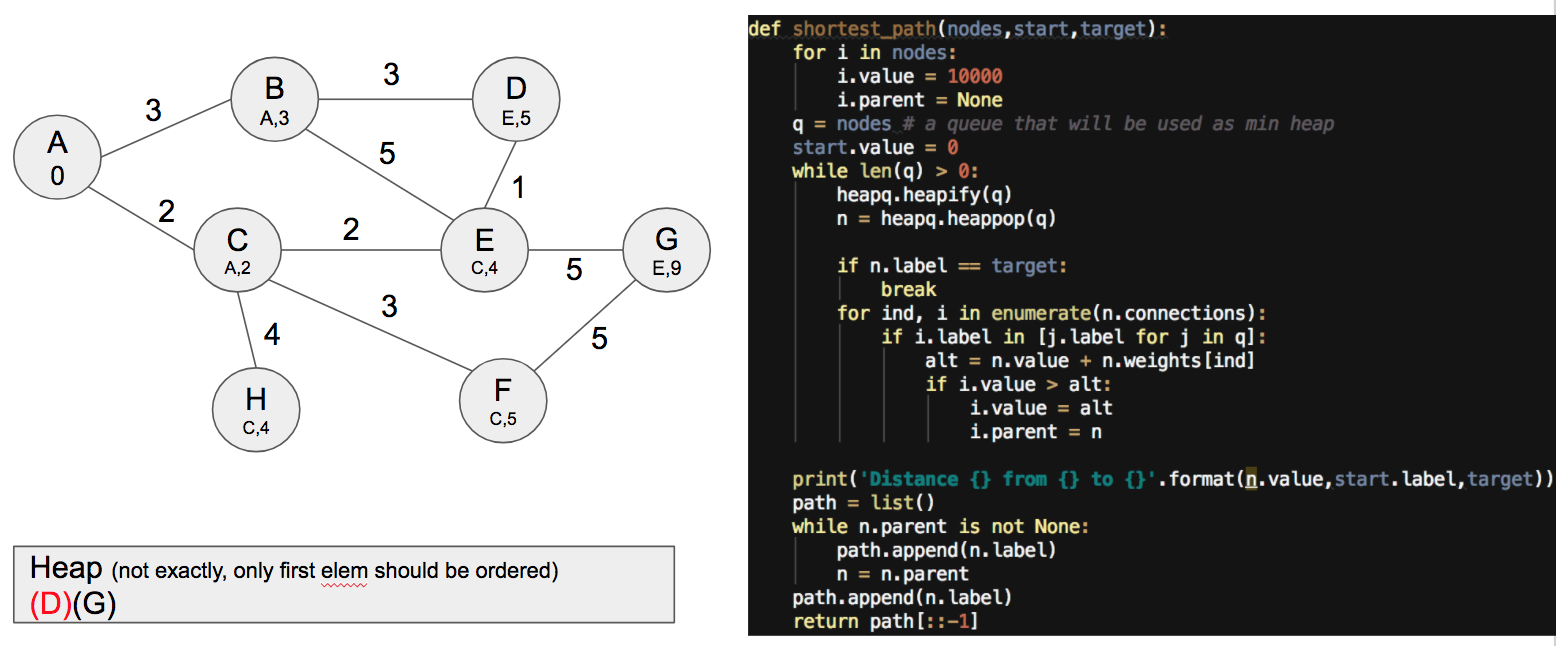
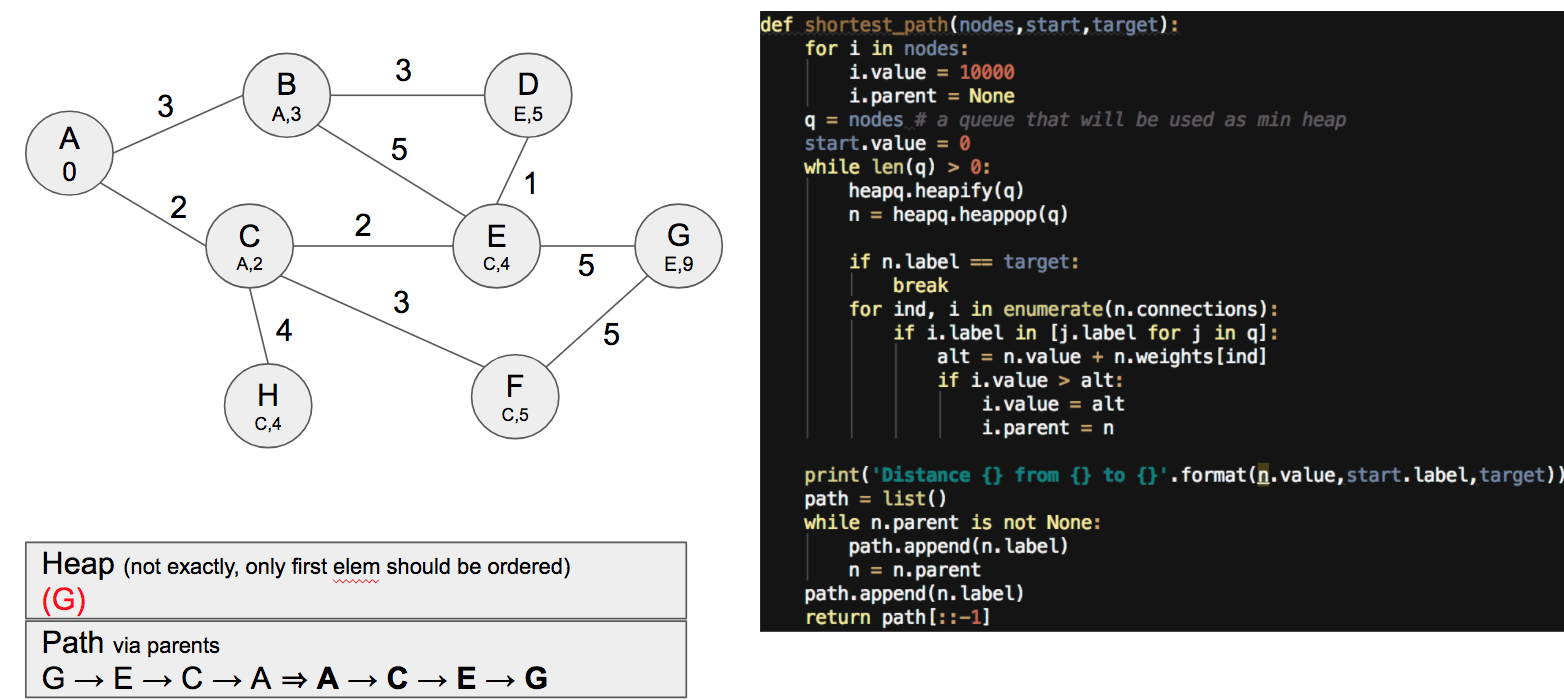
Ta-da! So we have it, now we can use a loop to get the path by using the attribute parent saved in each node.

Hope you enjoyed, and see you in the next post!

PS: these images are part of one huge Google slides document I manage. It's about Algorithms and tips and tricks and concepts for coding, especially to deal with coding exercises for interviews. Check it out if you have interest 🙂